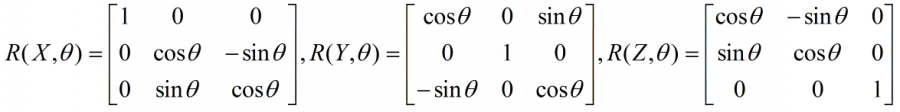产品:351
联系我们
我们采用这样的一个体系，即存在着一个世界坐标系，我们所定义的位姿都是参照世界坐标系或者由世界坐标系定义的笛卡尔坐标系。
1.位姿表示
位姿描述：
在机器人学中，位置和姿态经常成对出现，于是我们将此组合称作位姿，4个矢量成一组，表示了位置和姿态信息。并用它们来描述坐标系，即一个坐标系可以等价地用一个位置矢量和一个旋转矩阵来描述。
位置：x、y、z坐标
姿态：刚体与OX轴的夹角rx、与OY轴的夹角ry、与OZ轴的夹角rz
假设基坐标系为OXYZ，刚体坐标系为O`X`Y`Z`。对于机器人而言，空间中的任何一个点都必须要用上述六个参数明确指定，即(x,y,z,rx,ry,rz)，即便(x,y,z)都一样，(rx,ry,rz)不同代表机器人以不同的姿态去到达同一个点。
刚体的位置可以用一个3x1的矩阵来表示，即刚体坐标系中心O`在基坐标系中的位置，即
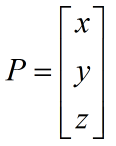
刚体的姿态可以用一个3x3的矩阵来表示，即刚体坐标系在基坐标系中的姿态，即
其中，***列表示刚体坐标系的O`X`轴在基坐标系的三个轴方向上的分量，称为单位主矢量。同理，第二列和第三列分别是刚体坐标系的O`Y`轴和O`Z`轴在基坐标系的三个轴方向上的分量。
举个例子，在下图中，刚体M沿坐标系O中平移了（0,20,15），绕Z轴旋转了90度，因此刚体M在坐标系O的位姿可描述为：
，
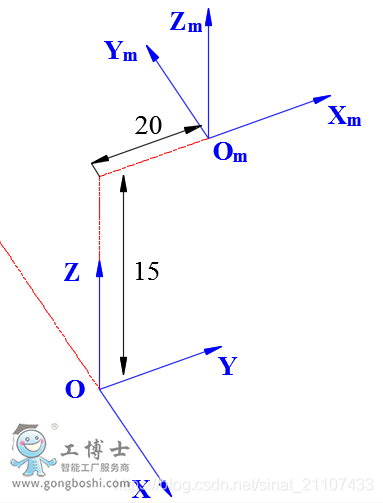
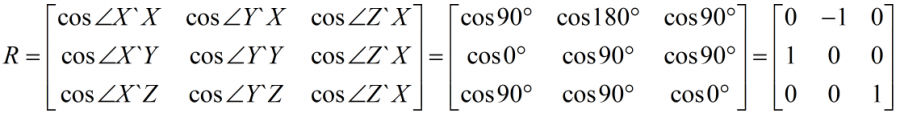
根据上面的例子，很容易得到，刚体坐标系绕X轴（Y轴、Z轴）旋转角度θ后的姿态矩阵为：
